On LinkedIn, you can play a variant of the N-Queens problem. A community version of the puzzle can be found here.
An example puzzle looks like this:
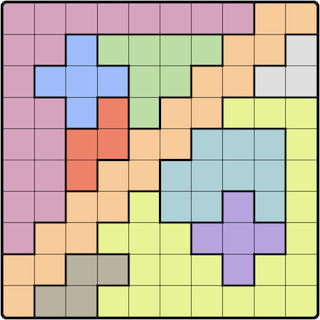
The idea is that each row, column, and colored region must contain exactly one queen. Queens cannot be placed in adjacent cells, including diagonally.
Recently, we saw it solved using:
I wanted to solve it using the CP-SAT constraint programming solver, which is part of Google’s OR Tools.
Installing this in a Python environment is easy: uv add ortools requests.
Next, we set up some basic information and fetch a level:
from ortools.sat.python import cp_model
import requests
import re
import ast
level_source = requests.get(
"https://raw.githubusercontent.com/samimsu/queens-game-linkedin/"
+ "refs/heads/main/src/utils/levels/level1.ts"
).text
match = re.search(
r"colorRegions:\s*(\[[^\]]+\](?:,\s*\[[^\]]+\])*)", level_source, re.DOTALL
)
LEVEL = ast.literal_eval(f"{match.group(1)}]")
ZONES = set([letter for row in LEVEL for letter in row])
ROWS = len(LEVEL)
COLS = len(LEVEL[0])
I’m just grabbing the level file from the aforementioned community version of the puzzle. The other levels are in the GitHub repo.
Next, we set up the model and create boolean variables indicating whether a position has a queen or not:
model = cp_model.CpModel()
solution = [
[model.NewBoolVar(f"x_{r}_{c}") for c in range(COLS)] for r in range(ROWS)
]
Next, we add the basic constraints: only one queen per row, column, and colored region:
# Exactly one per row
for r in range(ROWS):
model.Add(sum(solution[r][c] for c in range(COLS)) == 1)
# Exactly one per column
for c in range(COLS):
model.Add(sum(solution[r][c] for r in range(ROWS)) == 1)
# Exactly one per region
for letter in ZONES:
model.Add(
sum(
solution[r][c]
for r in range(ROWS)
for c in range(COLS)
if LEVEL[r][c] == letter
)
== 1
)
Finally, queens cannot touch each other, including on the diagonals. Since the previous constraints already cover horizontal and vertical touching, we only need to prohibit a queen to be present diagonally in the row below a given queen. We don’t need to prohibit the row above as this is symmetric.
# No queens on the same diagonal
for r in range(ROWS - 1):
for c in range(COLS):
if c > 0:
model.Add(solution[r + 1][c - 1] == 0).OnlyEnforceIf(solution[r][c])
if c < COLS - 1:
model.Add(solution[r + 1][c + 1] == 0).OnlyEnforceIf(solution[r][c])
And finally we can solve and print out a solution:
def pr_sol(sol, solution):
for r in range(ROWS):
for c in range(COLS):
if sol.Value(solution[r][c]) > 0:
print(f" *{LEVEL[r][c]}* ", end="")
else:
print(f" {LEVEL[r][c].lower()} ", end="")
print("")
print("\n\n")
solver = cp_model.CpSolver()
solver.parameters.log_search_progress = True
result = solver.Solve(model)
pr_sol(solver, solution)
Success:
CpSolverResponse summary:
status: OPTIMAL
walltime: 0.003608
usertime: 0.003608
deterministic_time: 4.7637e-05
gap_integral: 0
a a b *B* b c c c
a d b d b *E* c c
a *D* b d b c c c
a d d d b f g *C*
*A* d d d b f g g
a d *H* d b f g g
h d h d b f *F* g
h h h h *G* g g g
We can also easily confirm whether this is the only feasible solution:
class VarArraySolutionPrinter(cp_model.CpSolverSolutionCallback):
def __init__(self, variables):
cp_model.CpSolverSolutionCallback.__init__(self)
self.__variables = variables
def on_solution_callback(self):
pr_sol(self, self.__variables)
solver = cp_model.CpSolver()
solver.parameters.log_search_progress = True
solver.parameters.enumerate_all_solutions = True
result = solver.Solve(model, VarArraySolutionPrinter(solution))
Which indeed is the case:
Starting subsolver 'main' hint search at 0.01s
Starting subsolver 'main' search at 0.01s
#1 0.01s main
a a b *B* b c c c
a d b d b *E* c c
a *D* b d b c c c
a d d d b f g *C*
*A* d d d b f g g
a d *H* d b f g g
h d h d b f *F* g
h h h h *G* g g g
#Done 0.01s main
Bonus: Tango
LinkedIn also has another puzzle, called Tango, which looks like this:
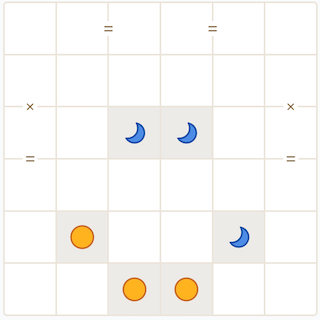
With these rules: fill each cell with either a sun or moon. No more than two of the same symbol may be next (vertically or horizontally) to each other. Each row and column must have an equal number of suns and moons. Cells separated by “=” must be the same type. Cells separated by “×” must be opposite types.
This is also easy to solve with constraint programming (as a Mixed Integer Program it is a bit harder but also possible). First we prepare the level data and some constants. No easy way to load in level data in this case, so we just define it hardcoded:
level = """
......
......
..00..
......
.1..0.
..11..
"""
equal = [
[(0, 1), (0, 2)],
[(0, 3), (0, 4)],
[(2, 0), (3, 0)],
[(2, 5), (3, 5)],
]
opposite = [
[(1, 0), (2, 0)],
[(1, 5), (2, 5)],
]
LEVEL = [
[int(nr) if nr != "." else -1 for nr in row]
for row in level.strip().split("\n")
if row
]
ROWS = len(LEVEL)
COLS = len(LEVEL[0])
0 is a moon and 1 is a sun (or vice versa). The dots are empty spots and get converted to -1. Next we set up the solution variables which can just be bools:
model = cp_model.CpModel()
solution = [[model.NewBoolVar(f"x_{r}_{c}") for c in range(COLS)] for r in range(ROWS)]
And then we can add the constraints:
# Set known values
for r in range(ROWS):
for c in range(COLS):
if LEVEL[r][c] != -1:
model.Add(solution[r][c] == LEVEL[r][c])
# No more than three in a row and col
for r in range(ROWS):
model.Add(sum([solution[r][c] for c in range(COLS - 2)]) < 3)
model.Add(sum([solution[r][c].Not() for c in range(COLS - 2)]) < 3)
for c in range(COLS):
model.Add(sum([solution[r][c] for r in range(ROWS - 2)]) < 3)
model.Add(sum([solution[r][c].Not() for r in range(ROWS - 2)]) < 3)
# Equality and opposite constraints
for eq in equal:
model.Add(solution[eq[0][0]][eq[0][1]] == solution[eq[1][0]][eq[1][1]])
for neq in opposite:
model.Add(solution[neq[0][0]][neq[0][1]] != solution[neq[1][0]][neq[1][1]])
And then can run the solver and print out the solution:
def pr_sol(sol, solution):
for r in range(ROWS):
for c in range(COLS):
val = sol.Value(solution[r][c])
print(f" {val} ", end="")
print("")
print("\n\n")
solver = cp_model.CpSolver()
solver.parameters.log_search_progress = True
result = solver.Solve(model)
pr_sol(solver, solution)
0 1 1 0 0 0
0 0 1 1 0 0
1 1 0 0 1 1
1 0 0 1 1 1
0 1 0 1 0 0
0 0 1 1 0 0
Here too, the presolver of CP-SAT can immediately reduce this to a trivial problem without having to run any further search.
Bonus: Zip
LinkedIn also has another puzzle, called Zip, which looks like this:
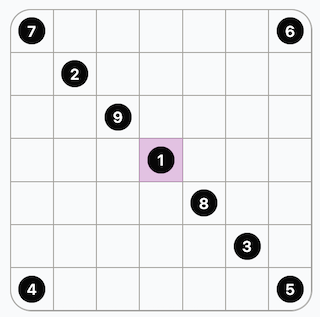
With these rules: draw a single path that fills every cell. Follow the numbered cells in order.
It seems that additionally paths start at 1 and end at the highest number. This problem is a little bit more interesting as it basically involves finding a Hamiltonian cycle, but with CP-SAT that is pretty easy.
level = """
1.....
....7.
.4.8..
..6.5.
.3....
.....2
"""
LEVEL = [
[int(nr) if nr != "." else 0 for nr in row]
for row in level.strip().split("\n")
if row
]
NUMBERS = set([int(nr) for row in LEVEL for nr in row if nr != "."])
ROWS = len(LEVEL)
COLS = len(LEVEL[0])
model = cp_model.CpModel()
solution = [
[model.NewIntVar(1, ROWS * COLS, f"x_{r}_{c}") for c in range(COLS)]
for r in range(ROWS)
]
We will use integer variables as our solution variables here, basically numbering each cell from 1 to ROWS*COLS to indicate the order in which they are visited.
Making sure that we visit the numbers in the right order is easy enough:
# Enforce ordering of known numbers
from itertools import product
for r1, c1 in product(range(ROWS), range(COLS)):
for r2, c2 in product(range(ROWS), range(COLS)):
if (r1, c1) == (r2, c2) or LEVEL[r1][c1] == 0 or LEVEL[r2][c2] == 0:
continue
if LEVEL[r1][c1] < LEVEL[r2][c2]:
model.Add(solution[r1][c1] < solution[r2][c2])
if LEVEL[r1][c1] == 1:
model.Add(solution[r1][c1] == 1)
if LEVEL[r1][c1] == max(NUMBERS):
model.Add(solution[r1][c1] == ROWS * COLS)
But this doesn’t lead to a valid path (we can just jump over neighbors). So to make sure our path is valid, we construct a Hamiltonian cycle. Probably an alternative method is constraining each cell to have neighbor equal to itself minus one (except for the starting position) and a neighbor to itself plus one (except for the ending position), but this leads to having to manually introduce a bunch of helper variables so just using the constraints CP-SAT provides is easier:
# Construct Hamiltonian cycle
arcs = []
pos_to_nr = {
(r, c): i for i, (r, c) in enumerate(product(range(ROWS), range(COLS)))
}
nr_to_pos = {
i: (r, c) for i, (r, c) in enumerate(product(range(ROWS), range(COLS)))
}
offsets = [(0, -1), (0, +1), (-1, 0), (+1, 0)]
for (r, c), number in pos_to_nr.items():
lit_to = model.NewBoolVar(f"lit_{r}_{c}_to_dummy")
lit_from = model.NewBoolVar(f"lit_{r}_{c}_from_dummy")
arcs.append((number, len(nr_to_pos), lit_to))
arcs.append((len(nr_to_pos), number, lit_from))
for offset in offsets:
nr, nc = r + offset[0], c + offset[1]
if nr < 0 or nc < 0 or nr >= ROWS or nc >= COLS:
continue
lit = model.NewBoolVar(f"lit_{r}_{c}_{nr}_{nc}")
# If this arc is chosen in our path then the neighbor must be one higher than this cell
model.Add(solution[nr][nc] - solution[r][c] == 1).OnlyEnforceIf(lit)
arcs.append((number, pos_to_nr[(nr, nc)], lit))
model.add_circuit(arcs)
In case you’re wondering how this works in terms of this being a closed “cycle”: the first and last cell are connected to a “dummy” cell.
Solving:
def pr_sol(sol, solution):
chars = ["←", "→", "↑", "↓", "."]
for r in range(ROWS):
for c in range(COLS):
val = sol.Value(solution[r][c])
for oi, offset in enumerate(offsets):
nr, nc = r + offset[0], c + offset[1]
if nr < 0 or nc < 0 or nr >= ROWS or nc >= COLS:
continue
val_neigh = sol.Value(solution[nr][nc])
if val_neigh == val + 1:
break
else:
oi = 4
print(
f" {chars[oi]}{LEVEL[r][c] or ' '} ", end=""
)
print("")
print("\n\n")
solver = cp_model.CpSolver()
solver.parameters.log_search_progress = True
result = solver.Solve(model)
pr_sol(solver, solution)
↓1 → → → → ↓
↓ ↑ → → ↓7 ↓
↓ ↑4 ↑ .8 ← ↓
↓ ↑ ↑6 ← ←5 ←
↓ ↑3 ← ← ← ←
→ → → → → ↑2
This problem cannot be fully reduced during the presolve:
Preloading model.
#Model 0.01s var:136/137 constraints:221/221
Starting search at 0.01s with 16 workers.
CpSolverResponse summary:
status: OPTIMAL
objective: NA
best_bound: NA
integers: 34
booleans: 109
conflicts: 54
branches: 808
propagations: 5261
integer_propagations: 7070
restarts: 427
lp_iterations: 0
walltime: 0.013788
usertime: 0.013788
deterministic_time: 0.0410384
gap_integral: 0
The actual version of the puzzle also introduces walls in some levels that cannot be crossed by the path, but this is trivial to add, essentialy something like:
if (r, c, nr, nc) in walls or (nr, nc, r, c) in walls:
model.Add(lit == 0)
In the for loop above.