TL;DR: very likely not.

A student once asked me whether it would make sense to tune the probability cutoff (a.k.a. threshold) for trees in a random forests. Let’s explain first what we mean by that exactly. Assume a binary classification setting. Say we’ve trained a single decision tree. We know that the prediction is given by the leaf node, and that a probability P(y=1|x) can be assigned by the number of training examples in leaf node with positive outcome divided by the number of all training examples in leaf node (note that this is a fixed ratio for each leaf node and does not change once the tree is trained). This is not a well-calibrated probability, but does allow to rank predictions.

Given such a probability P(y=1|x), it is then possible to specify a threshold T so that if P(y=1|x) >= T, we assume the outcome to be 1, and 0 otherwise. We can then tune T (e.g. through cross-validation) to get an optimal cutoff point given a metric we desire to optimise (accuracy, F1, or something else…) ¹.

Let us now consider the case of a random forest: N trees are constructed which all provide their prediction for a given instance, after which the majority vote determines the final outcome. Again, a probability P(y=1|x) can be assigned as the number of trees which predicted y=1 divided by N.

However, we’ve kind of forgotten about the fact that every tree member itself can output a probability as well. What if we would tune the individual trees with a threshold Tn, with n = 1..N? Would this lead to a better result? The answer is that it might, but only in very specific circumstances, and is hence probably not worth doing.

First, most implementations of random forest construct non-pruned trees. E.g. each leaf node relates to one training example. This doesn’t lead to overfit thanks to bootstrapping and random feature subset selection. As such, the probability that P(y=1|x) is either 1 or 0 for each tree, and threshold tuning would not make sense here.

Second, many implementations (most notably scikit-learn) in fact deviate from the behavior of random forests as originally described. Instead of letting each tree vote and having the final probability of the ensemble equal P(y=1|x) = number of trees which predicted y=1 / N, they instead average the probabilistic predictions of all members, i.e. P(y=1|x) = Σ(for n = 1..N)[ Pn(y=1|x) ] / N. This also avoids the problem of individual tree tuning altogether.

If you’re curious, see this tech report by Leo Breiman. Using averaging gives smoother probabilities. Again, note that this doesn’t matter under the default assumption where we build trees all the way down.

But what happens if we do limit the depth of trees?

This is easily tested, e.g. by means of the following example churn data set:

df = pd.read_csv("https://raw.githubusercontent.com/yhat/demo-churn-pred/master/model/churn.csv")
df.drop(columns=['Phone', 'State'], inplace=True)
df['Int\'l Plan'].replace({'no': 0, 'yes': 1}, inplace=True)
df['VMail Plan'].replace({'no': 0, 'yes': 1}, inplace=True)
df['Churn?'].replace({'False.': 0, 'True.': 1}, inplace=True)

np.unique(df['Churn?'], return_counts=True)
# (array([0, 1], dtype=int64), array([2850,  483], dtype=int64))

X, y = df.drop(columns=['Churn?']), df['Churn?']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5)

Training a standard random forest with limited depth:

rf = RandomForestClassifier(max_depth=2).fit(X_train, y_train)
base_score = roc_auc_score(
    y_test,
    rf.predict_proba(X_test)[:,1]
)

print("RF AUC:", base_score)
# RF AUC: 0.8785843604842545

We can then implement our own predict function which accepts a threshold:

def rf_predict_thresholded(model, X, average=True, tree_threshold=0.5):
    # tree_threshold is ignored if average=True
    preds = []
    for estimator in rf.estimators_:
        preds.append(np.array(estimator.predict_proba(X)[:,1]))
    P = np.vstack(preds).T
    if average:
        V = np.mean(P, axis=1)
    else:
        P[P >= tree_threshold] = 1; P[P < tree_threshold] = 0
        V = np.sum(P, axis=1) / len(rf.estimators_)
    return V

And comparing it with the original score:

auc_avg = roc_auc_score(y_test, rf_predict_thresholded(rf, X_test))
auc_thr = roc_auc_score(y_test, rf_predict_thresholded(rf, X_test, average=False))

print("RF AUC (scikit-learn):", base_score)
print("RF AUC (manual implementation):", auc_avg)
print("RF AUC (0.5 threshold):", auc_thr)

# RF AUC (scikit-learn):          0.8785843604842545
# RF AUC (manual implementation): 0.8785843604842545
# RF AUC (0.5 threshold):         0.8740978140277726

We get the same result, and see that the majority voting approach even does slightly worse with a threshold of 0.5. We can in fact see that the average probabilities differ somewhat from the majority voted ones in this case:

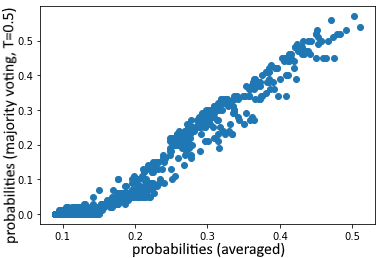
We can then tune the threshold (on the training set, to play it safe, but you’d normally cross-validate this):

thresholds = np.linspace(0, 1, 30)

aucs = [roc_auc_score(
    y_train, 
    rf_predict_thresholded(rf, X_train, average=False, tree_threshold=t)
) for t in thresholds]

best_thres = thresholds[np.argmax(aucs)]

print("Best threshold:", best_thres)
# Best threshold: 0.10344827586206896

plt.plot(thresholds, aucs)

Interestingly enough, the best threshold appears to be around 0.10:

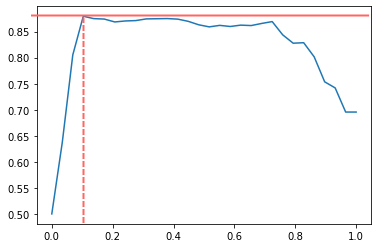
With these final test set results:

best_auc = roc_auc_score(
    y_test,
    rf_predict_thresholded(rf, X_test, average=False, tree_threshold=best_thres)
)

print("RF AUC (scikit-learn):", base_score)
print("RF AUC (manual implementation):", auc_avg)
print("RF AUC (0.5 threshold):", auc_thr)
print(f"RF AUC (best threshold = {best_thres}):", best_auc)

# RF AUC (scikit-learn):                         0.8951299611518283
# RF AUC (manual implementation):                0.8951299611518283
# RF AUC (0.5 threshold):                        0.8782447377605374
# RF AUC (best threshold = 0.10344827586206896): 0.8906157921536992

As can be seen, this best threshold comes close to our averaged value. When repeating the run with a different random seed, we can find cases where the best threshold does slightly better. So what to take from this?

• Tuning the threshold of individual trees is most likely not worth it
• Except when (for some reason) you’re using depth-limited trees and can not use an averaged ensemble prediction probability (but in which case it would be easier and better to implement that instead)
• It might play a more important role when incorporating less trees in the ensemble (in which case it’s better to use more trees)
• We’ve used the same threshold for every tree in the ensemble, but tuning this on a per-tree basis would lead even further down the rabbit hole (metalearning-like)

So in short: stick instead to the basics.