A friend of mine recently asked whether there was an easy way to introduce new levels (i.e. items) to an embedding layer in Keras and only training the embedding layer for those new levels, i.e. keeping the weights for the existing indices fixed.
Note that this is not necessarily a good idea: the presence of new levels typically indicates that your model is due for a full maintenance retraining. The context in which we were discussing this originally was in a singular value decomposition setup of users and items (as it common in a recommender system setting, for instance). The question was whether we could keep the item embedding space for existing items fixed when introducing new items. Note that here too, this is suboptimal (assuming new items are being rated by existing users 1), especially so when we also want to user embeddings to stay fixed.
Let us approach the problem using an easier setting. We will assume we have a data set X with every instance Xi = c with c ∈ 0..C with C our initial number of levels. We will train a model using an embedding layer to M(X) → y ∈ [0, 1] i.e. a binary classification model. We will then introduce a data set X’ with every instance X’i = c’ with c’ ∈ C+1..C’ and see how we can retrain our embedding layer.
First of all we need some imports:
from tensorflow import keras
from tensorflow.keras import backend as K
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Embedding, Flatten, Dense, Lambda, Reshape, Multiply, Add
from tensorflow.keras.regularizers import l2
import numpy as np
from pylab import cm
We will also construct a toy data set to work on. How this is created is not that important, but we split it up into an X and X’ as defined above (as well as the two combined):
# cat_idx_rs and y are provided
X_init, y_init = cat_idx_rs[cat_idx_rs<80], y[cat_idx_rs<80]
X_new, y_new = cat_idx_rs[cat_idx_rs>=80], y[cat_idx_rs>=80]
X_together = np.hstack([X_init, X_new])
y_together = np.hstack([y_init, y_new])
num_categories_init = len(np.unique(X_init)) # 80
num_categories_all = len(np.unique(X_together)) # 100
Note that X_init contains the levels indexed 0 up to 80 2, X_new contains levels indexed 80 up to 100.
Initial Model
So here is what an initial model would look like, trained on X_init and y_init:
def EmbeddingModel(num_categories, vector_dim=2, reg=False):
if reg is False: reg = l2(0.000001)
input_cat = Input((1,), name='input_cat')
i = Embedding(num_categories, vector_dim, input_length=1, name='embedding_cat',
embeddings_regularizer=reg, embeddings_initializer='random_normal')(input_cat)
i = Flatten()(i)
o = Lambda(lambda x : K.sigmoid(K.sum(x, axis=-1)))(i)
o = Reshape((1,))(o)
model = Model(inputs=input_cat, outputs=o)
model.compile(loss='binary_crossentropy', metrics=['accuracy'], optimizer='rmsprop')
return model
model = EmbeddingModel(num_categories_init)
# fit_with_lr is a simple helper function
fit_with_lr(model, X_init, y_init, lr=0.005, epochs=1)
fit_with_lr(model, X_init, y_init, lr=0.01, epochs=1)
# 89/89 [======] - 1s 4ms/step - loss: 0.6593 - accuracy: 0.6934 - val_loss: 0.6324 - val_accuracy: 0.7339
# 89/89 [======] - 0s 2ms/step - loss: 0.6008 - accuracy: 0.7404 - val_loss: 0.5810 - val_accuracy: 0.7397
We use an extremely simple prediction setup here where we just sum the embedding weights and push them through a sigmoid function to get our prediction. We could also have used a Dense layer obviously but is not necessary for the scope of this discussion.
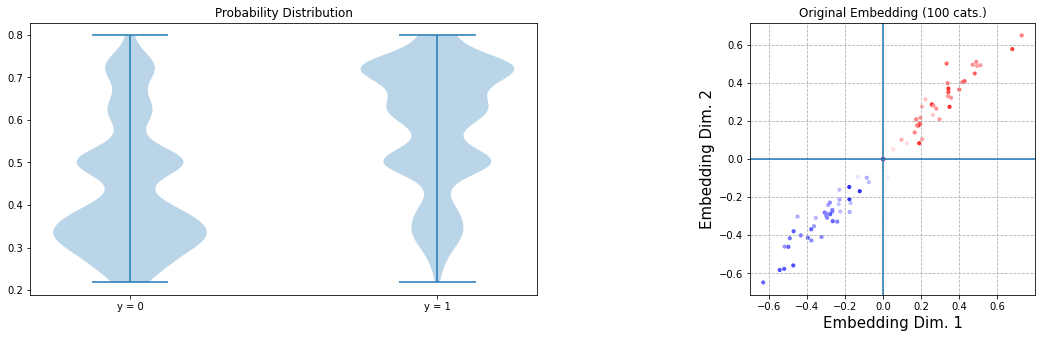
In any case, we get a good accuracy baseline. The figure below shows the probability distribution of the model on X_init (obviously, we’d normally use a test set) and — more interestingly — the embeddings for the 80 levels.
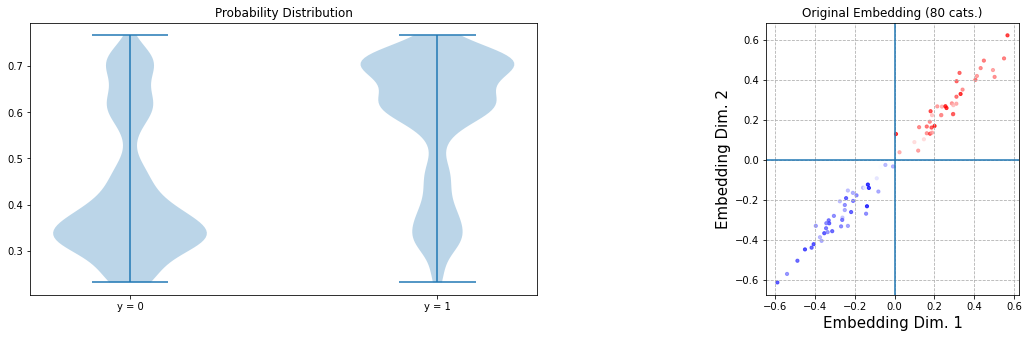
The colours give an indication of the true class labels and is calculated as the number of positive instances with the corresponding class label divided over the total number of instances with the corresponding class label. Grey is 50%, darker red more closer to 100%, darker blue closer to 0%. Note that blue is in the negative quadrant as this will result in a <0.5 probability output when pushed through the sigmoid function.
We will now take a look at three different ways how we can update this model to include embeddings for the 20 additional categories of X_new without retraining the existing ones.
Updated Model Using Two Embedding Layers
A first method is shown by the code below:
def EmbeddingModelIsNew(num_categories, previous_embedding_weights, vector_dim=2, reg=False):
if reg is False: reg = l2(0.000001)
num_previous_categories = previous_embedding_weights[0].shape[0]
num_new_categories = num_categories - num_previous_categories
num_max_categories = max(num_previous_categories, num_new_categories)
input_cat = Input((1,), name='input_cat')
input_cat_clamped = Lambda(lambda x : K.switch(K.less_equal(K.constant(num_previous_categories), x),
x - num_max_categories,
x))(input_cat)
input_cat_clamped = Reshape((1,))(input_cat_clamped)
input_new = Lambda(lambda x : K.switch(K.less_equal(K.constant(num_previous_categories), x),
K.ones_like(x),
K.zeros_like(x)))(input_cat)
input_new = Reshape((1,))(input_new)
i_old = Embedding(num_previous_categories,
vector_dim, input_length=1, name='embedding_cat_old',
embeddings_regularizer=reg, embeddings_initializer='random_normal')(input_cat_clamped)
i_old = Flatten()(i_old)
i_new = Embedding(num_max_categories,
vector_dim, input_length=1, name='embedding_cat_new',
embeddings_regularizer=reg, embeddings_initializer='random_normal')(input_cat_clamped)
i_new = Flatten()(i_new)
i_old = Multiply()([1-input_new, i_old])
i_new = Multiply()([input_new, i_new])
i = Add()([i_old, i_new])
o = Lambda(lambda x : K.sigmoid(K.sum(x, axis=-1)))(i)
o = Reshape((1,))(o)
model = Model(inputs=input_cat, outputs=o)
model.compile(loss='binary_crossentropy', metrics=['accuracy'], optimizer='rmsprop')
model.get_layer('embedding_cat_old').set_weights(previous_embedding_weights)
model.get_layer('embedding_cat_old').trainable = False
return model
new_model = EmbeddingModelIsNew(num_categories_all, model.get_layer('embedding_cat').get_weights())
fit_with_lr(new_model, X_new, y_new, lr=0.005, epochs=1)
fit_with_lr(new_model, X_new, y_new, lr=0.01, epochs=1)
Here, we do the following: we construct a new model with two embedding layers, one with the same number of categories as the initial model (80 in our case) and one with its categories set equal to the maximum of the old and new number of categories. Since both embedding layers assume the indexes to start at 0, we use a switch statement to subtract the maximum of the old and new number of categories in case the index exceeds the old number of levels. I.e. we will remap levels 80 to 100 → 0 to 20. So why don’t we use 20 categories in i_new? Well, since levels 20 to 80 might also still occur, and even though we won’t do anything with the embeddings created for these, we still need to include them. Next, since we now get two embeddings for each index, but only one is valid, we multiply with an additional binary input indicating whether the index is a new one or not, again derived by using a switch statement. Finally, we copy over the existing weights and set one embedding layer to be non-trainable.
So, in this situation: the old embedding layer will have 80 vectors, the new one will have max(80, 20) = 80 weights as well. The incoming indices 0-100 will be remapped to 0-80 so none of the embedding layers error out. Indices 0-20 are shared and can refer to either new or old indices, given by input_new, which will multiply one of the embeddings with 0 to cancel it out. Finally, since the old embedding layer won’t be retrained anyway, we can train using new indices only. We can however still make predictions on the complete data set (X_together) and indeed verify that the original embeddings didn’t change:
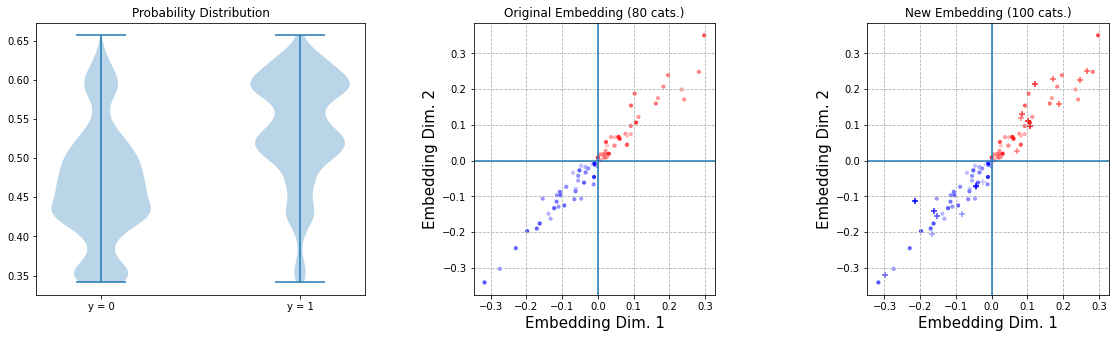
As an aside, you might wonder what would happen if we would introduce more new indices than we had old ones, e.g. assume that X_new had 100 new indices from 80-180: the old layer would still contain 80 vectors, and the new one would now have max(80, 100) = 100 weights. The incoming indices 0-180 would be remapped to 0-80 so again none of the embeddings would error out.
So this approach works and has the benefit that you can get it working using relatively basic Keras knowledge only, but is somewhat unwieldy. Especially the fact that the new embedding layer has more weights than we actually need is a pity.
Updated Model Using Custom Keras Class
Obviously, a more easier way is simply by extending the existing Embedding class:
import tensorflow.compat.v2 as tf
from tensorflow.python.ops import math_ops
from tensorflow.python.ops import embedding_ops
from tensorflow.python.keras import backend as K
from tensorflow.python.keras.utils import tf_utils
class ExtendingEmbedding(Embedding):
def __init__(self, input_dim, output_dim, input_dim_existing, **kwargs):
super(ExtendingEmbedding, self).__init__(input_dim, output_dim, **kwargs)
self.input_dim_existing = input_dim_existing
self.input_dim_new = input_dim - self.input_dim_existing
@tf_utils.shape_type_conversion
def build(self, input_shape=None):
self.embeddings_existing = self.add_weight(
shape=(self.input_dim_existing, self.output_dim),
initializer=self.embeddings_initializer,
name='embeddings_existing',
regularizer=self.embeddings_regularizer,
constraint=self.embeddings_constraint,
experimental_autocast=False,
trainable=False)
self.embeddings_new = self.add_weight(
shape=(self.input_dim_new, self.output_dim),
initializer=self.embeddings_initializer,
name='embeddings_new',
regularizer=self.embeddings_regularizer,
constraint=self.embeddings_constraint,
experimental_autocast=False)
self.built = True
def call(self, inputs):
dtype = K.dtype(inputs)
if dtype != 'int32' and dtype != 'int64':
inputs = math_ops.cast(inputs, 'int32')
emb = K.concatenate([self.embeddings_existing, self.embeddings_new], axis=0)
out = embedding_ops.embedding_lookup_v2(emb, inputs)
if self._dtype_policy.compute_dtype != self._dtype_policy.variable_dtype:
out = tf.cast(out, self._dtype_policy.compute_dtype)
return out
Again, this is perhaps a bit more cumbersome than we’d want it to be since we need two add_weight calls here. (A better name would be add_weight_tensor since we’re adding a shape of weights, but anyway.) One to hold the existing weights (set to non-trainable), and another one to provide room for the new levels. This would be easier if Keras would allow to set a part of a weights tensor to be non-trainable, but it makes sense that this is not feasible (most likely, it wouldn’t work well with vectorized operations on the GPU).
In any case we can now directly use this class as follows:
def EmbeddingModelCustom(num_categories, previous_embedding_weights, vector_dim=2, reg=False):
if reg is False: reg = l2(0.000001)
num_previous_categories = previous_embedding_weights[0].shape[0]
num_new_categories = num_categories - num_previous_categories
input_cat = Input((1,), name='input_cat')
i = ExtendingEmbedding(num_categories, vector_dim,
input_dim_existing=num_previous_categories,
input_length=1, name='embedding_cat',
embeddings_regularizer=reg, embeddings_initializer='random_normal')(input_cat)
i = Flatten()(i)
o = Lambda(lambda x : K.sigmoid(K.sum(x, axis=-1)))(i)
o = Reshape((1,))(o)
model = Model(inputs=input_cat, outputs=o)
model.compile(loss='binary_crossentropy', metrics=['accuracy'], optimizer='rmsprop')
K.set_value(model.get_layer('embedding_cat').embeddings_existing, previous_embedding_weights[0])
return model
new_model = EmbeddingModelCustom(num_categories_all, model.get_layer('embedding_cat').get_weights())
fit_with_lr(new_model, X_new, y_new, lr=0.005, epochs=1)
fit_with_lr(new_model, X_new, y_new, lr=0.01, epochs=1)
Again we only need to train on the new instances here as the existing weights won’t be retrained anyway. (Remark for the observant reader: in case other learnable parameters would be present such as a Dense layer, you might want to mix-in existing instances as well given that you allow those parameters to stay trainable.)
And then we get this result:
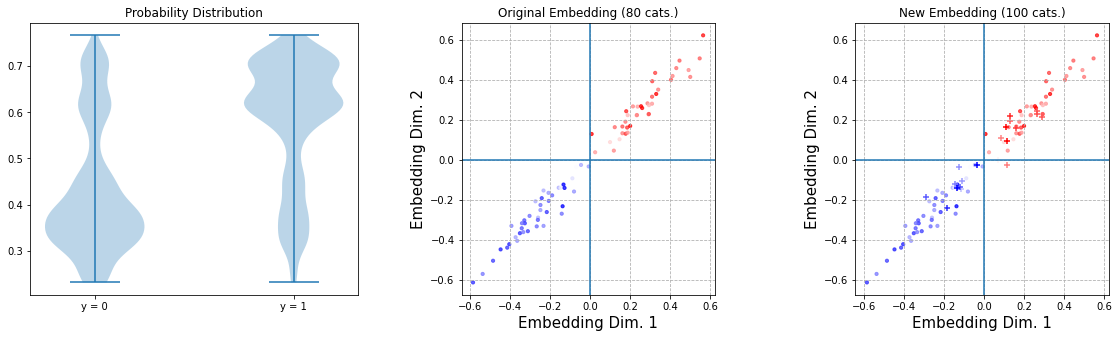
Updated Model Using Custom Keras Constraint
A third approach consists of using a Keras constraint to lock some of the weights in place whilst still keeping a full expanded embedding layer trainable. First, we define our constraint:
from tensorflow.keras.constraints import Constraint
class FixWeights(Constraint):
def __init__(self, weights):
self.weights = weights
def __call__(self, w):
r = K.concatenate([self.weights, w[self.weights.shape[0]:]], axis=0)
return r
And again can use this as follows:
def EmbeddingModelConstrained(num_categories, previous_embedding_weights, vector_dim=2, reg=False):
if reg is False: reg = l2(0.000001)
num_previous_categories = previous_embedding_weights[0].shape[0]
num_new_categories = num_categories - num_previous_categories
input_cat = Input((1,), name='input_cat')
constraint = FixWeights(previous_embedding_weights[0])
i = Embedding(num_categories, vector_dim,
embeddings_constraint=constraint,
input_length=1, name='embedding_cat',
embeddings_regularizer=reg, embeddings_initializer='random_normal')(input_cat)
i = Flatten()(i)
o = Lambda(lambda x : K.sigmoid(K.sum(x, axis=-1)))(i)
o = Reshape((1,))(o)
model = Model(inputs=input_cat, outputs=o)
model.compile(loss='binary_crossentropy', metrics=['accuracy'], optimizer='rmsprop')
return model
new_model = EmbeddingModelConstrained(num_categories_all, model.get_layer('embedding_cat').get_weights())
fit_with_lr(new_model, X_new, y_new, lr=0.005, epochs=1)
fit_with_lr(new_model, X_new, y_new, lr=0.01, epochs=1)
By the way, now comes the point at which is becomes clear why I have added in a very slight L2 regularization. If kept to None, using a constraint on an Embedding layer bugs out with: Cannot use a constraint function on a sparse variable.. TensorFlow is aware of the issue, with some people suggesting to use the constraint as a normal layer operation instead, as in:
emb = Embedding(input_dim, output_dim, name='embedding_name')
norm_layer = UnitNorm(axis=1)
norm_embedding = norm_layer(emb(embedding_id_input))
Err… that might work for a UnitNorm constraint (and I’m not sure, even), but definitely didn’t for FixWeights, so I doubt that this usage is correct. Strangely enough, setting a regularizer bypasses the issue and we get our result:
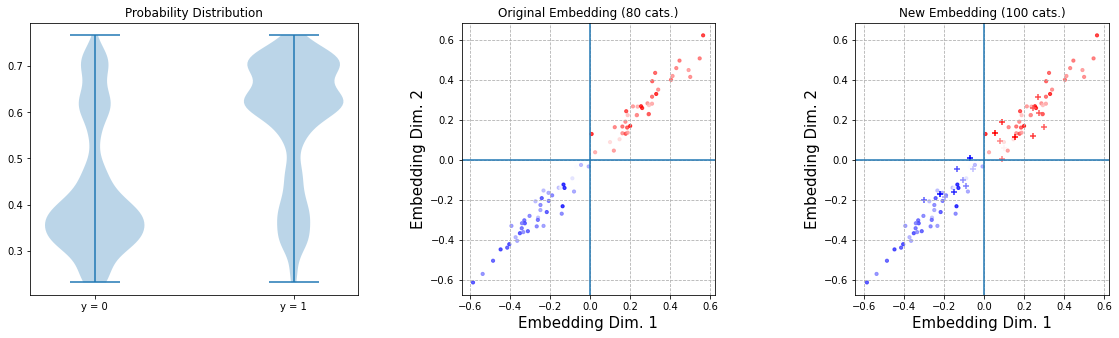
Full Retraining
So there you have it: three different ways on how to iteratively update an embedding layer. Just for fun, we can also compare the results above with the result a fully retrained model would give us:
new_model = EmbeddingModel(num_categories_all)
fit_with_lr(new_model, X_together, y_together, lr=0.002, epochs=1)
fit_with_lr(new_model, X_together, y_together, lr=0.001, epochs=1)
We can also take a look at how the embeddings jump around from one the original model to the new one using all indices:
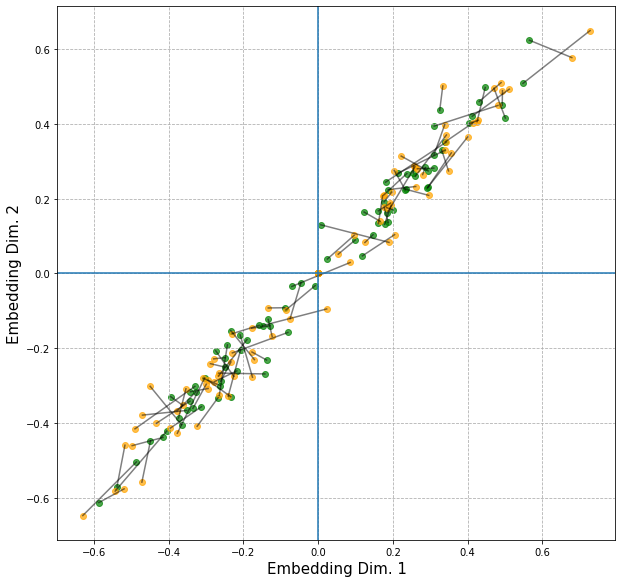
The green dots show the embedding for the initial model, and the orange dots for the new one. Lines connect embeddings for the same index (if included in both models). Even although the embedding is relatively stable here, this is of course mainly due to the way how we used it here (addition and sigmoid).