(This is part 5 in the Modern Genetic Algorithms Explained series, click here to go to the first post, or browse through all the parts with the Table Of Contents at the end of this post.)

First, let’s go to Wikipedia for a definition:

The ant colony optimization algorithm (ACO), is a probabilistic technique for solving computational problems which can be reduced to finding good paths through graphs. This algorithm is a member of Ant colony algorithms family, in Swarm intelligence methods, and it constitutes some metaheuristic optimizations. Initially proposed by Marco Dorigo in 1992 in his PhD thesis [1] [2] , the first algorithm was aiming to search for an optimal path in a graph; based on the behavior of ants seeking a path between their colony and a source of food. The original idea has since diversified to solve a wider class of Numerical problems, and as a result, several problems have emerged, drawing on various aspects of the behavior of ants.

“Good paths through graphs”. I have not converted our sample problem from the previous posts to a graphing problem. So no Python sample this time, sorry.

You do get to see some pseudocode though:

Given a number of nodes
Given some edges between nodes (paths)
Given BT := {}, this will contain our best tour
Randomly construct a tour T
Create a number of "ants" (often equal to number of nodes)
Associate a distance, pheromone value, and delta pheromone value to every edge
Iterate until time limit hit or satisfiable solution found:
  For each ant do:
    Do until tour constructed:
    Next node is chosen depending on visibility (e.g. 1/distance) and pheromone trail
    E.g. choose next node with probability (visibility^a)*(pheromone trail^b)
    Calculate fitness of this tour
    Copy this tour to the best tour if fitness is better
    Update the pheromone trail of each edge of this ant's tour:
    E.g. delta pheromone for edge := 1/(tour cost)
  For each edge:
    Lower pheromone value by a factor
    Add delta pheromone value to pheromone value
    Set delta pheromone := 0

ACO is an interesting method, again, we see certain aspects already used in the previous posts, like using pheromone trails to avoid local maxima. Since the algorithm is closely tied to graphs, nodes and paths, it’s no wonder it’s often used to find shortest paths, or to solve the traveling salesman problem.

There are some interesting links on the Wikipedia page, one of them is this application:

After a while, an ant finds a path to the food and places pheromones:

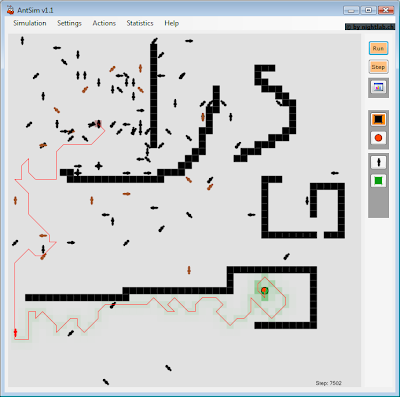
Those who are interested can read more about Swarm intelligence or Particle swarm optimization.

Table Of Contents (click a link to jump to that post)

1- Introduction 2- Genetic Algorithms 3- CHC Eshelman 4- Simulated Annealing 5- Ant Colony Optimization 6- Tabu Search 7- Conclusion